E’ del tutto ovvio e comune che Paola Ceccarelli e Enrico Balducci (nomi di fantasia) si siano sposati l’anno scorso a Roma, ma se analizziamo le contingenze successive che hanno reso possibile questo particolare evento ci rendiamo facilmente conto che la sua probabilità di occorrenza tende a zero. Infatti dovremmo calcolare la probabilità che quel particolare etrusco si sia invaghito, molte generazioni fa, di quella particolare sannita incontrata a una fiera e via via per generazioni, con una catena lunghissima di eventi, la cui composizione esatta (basta che salti un anello e tutto va a rotoli) è unica e quindi ‘impossibile’ dal punto di vista del calcolo delle probabilità. Se invece limitiamo le nostre pretese, sfuochiamo un pochino l’obiettivo, e ci chiediamo quale è la probabilità che due ragazzi di circa trenta anni di età si sposino a Roma, possiamo fare dei calcoli ragionevoli e arrivare a una probabilità statistica abbastanza precisa. Paola ed Enrico sono scomparsi nella loro unicità e sono stati dissolti nella classe dei ‘cittadini romani dai 25 ai 35 anni’: solo così la previsione ha senso.
Queste semplici considerazioni sono alla base dell’arte dell’analisi statistica dei dati da cui traiamo, per i nostri scopi, la definizione di due semplici indici: la media e la deviazione standard.
Senza entrare in particolari, qui ci basti dire che la media corrisponde alla somma dei valori presi da una misura di interesse X (e.g. peso, altezza, temperatura..) su un insieme di numerosità N di osservazioni indipendenti, diviso per il valore N, in formule:
rn
Media (X) = SUMn (Xi) / N
La deviazione standard è invece un ‘indice di dispersione’: ci fornisce delle informazioni sull’ entità delle deviazioni dalla media all’interno della popolazione. Insomma se una popolazione di altezza media 1.75 è formata da individui tutti più o meno alti uguale (bassa deviazione standard) oppure risulta da una popolazione molto eterogena che comprende anche soggetti molto alti e molto bassi. In formule:
rn
Dev. Stand.(X) = √ SUMn (Xi – Media(X))2/N
L’Egitto era detto dagli antichi ‘Il dono del Nilo’, il paese era infatti reso fertile dalle inondazioni del grande fiume che, circa due volte l’anno, trasformavano le sue aride sponde in campi fertilissimi grazie alla deposizione del ‘limo’, terra umida e grassa che permetteva abbondanti raccolti.
L’entità di ogni inondazione era proporzionale all’estensione del limo depositato, questa estensione era accuratamente misurata dagli impiegati governativi che, su tale base valutavano l’entità delle riserve alimentari (cfr. Genesi,41:17, dove l’interpretazione data da Giuseppe al sogno del Faraone delle sette vacche grasse seguite dalle sette vacche magre risulta coerente con le periodicità delle fluttuazioni delle inondazioni del Nilo poi verificate da Hurst).
Analizzando l’accurata documentazione storica dei livelli di massima e di minima delle piene del fiume, Hurst scoprì un interessante fenomeno: invece di una alternanza casuale di annate buone e annate cattive, sorprendentemente, rilevò che l’instaurarsi di una buona annata era seguita da altri anni con buon livello di acqua e, analogamente, l’inizio di scarsità di acqua persisteva per alcuni anni successivi (le vacche magre e grasse del sogno del Faraone, appunto). La figura di seguito, è un disegno originale di Hurst.
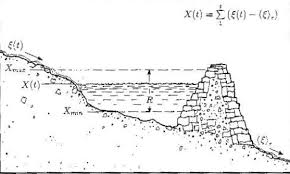 La grandezza R corrisponde all’’evento eccezionale, pari al valore più grande di escursione tra minima (Xmin) e massima (Xmax) portata del fiume, mentre in alto a destra riconosciamo una nostra conoscenza (la deviazione standard o ).
La grandezza R corrisponde all’’evento eccezionale, pari al valore più grande di escursione tra minima (Xmin) e massima (Xmax) portata del fiume, mentre in alto a destra riconosciamo una nostra conoscenza (la deviazione standard o ).
Hurst, invece di affrontare l’impossibile impresa di prevedere l’accadimento della piena eccezionale, prova a stimare la sua entità. Tutto sommato si trattava di costruire una diga che, se ben dimensionata, sarebbe stata in grado di contenere una piena eccezionale in qualsiasi momento fosse arrivata.
rn
Questo però non è vero per i valori estremi che, a differenza dalle proprietà medie, non si calcolano sull’intera distribuzione, ma da poche (anche una sola) osservazioni eccezionali. In questo caso l’aumentare di N non provoca nessuna convergenza verso un valore unico ma, al contrario, il continuo “spostarsi dell’asticella” della misura: più osservazioni raccolgo, maggiore sarà la probabilità di osservare eventi eccezionali. In altre parole, se aumento il numero n delle osservazioni, dopo un po’ (n abbastanza grande) il valore di media e deviazione standard della serie rimarranno sostanzialmente identici (è quella che popolarmente si chiama ‘legge dei grandi numeri’) mentre il valore del Range (R = Xmax – Xmin) tende a crescere per motivi puramente matematici (ogni osservazione ‘più estrema’ fa crescere R, che altrimenti resta identico, ma per definizione non può diminuire).
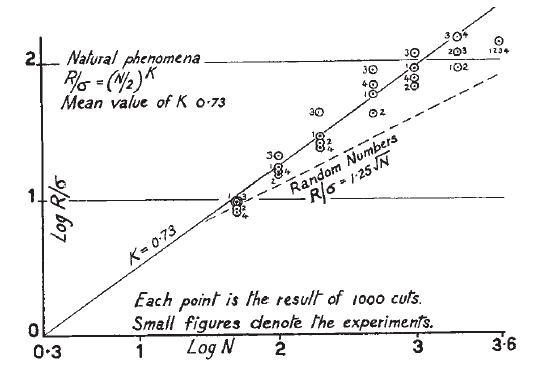 E’ il processo alla base della figura qui riportata tratta dall’articolo originale di Hurst del 1957 che ha come ascissa la lunghezza della serie (in unità logaritmiche) e in ordinata il rapporto tra Range e Deviazione Standard (R/) sempre in unità logaritmiche.
E’ il processo alla base della figura qui riportata tratta dall’articolo originale di Hurst del 1957 che ha come ascissa la lunghezza della serie (in unità logaritmiche) e in ordinata il rapporto tra Range e Deviazione Standard (R/) sempre in unità logaritmiche.
rn
Ma qui andiamo fuori dal seminato (anche se è la parte che interessa di più al vostro articolista), quello che conta è che la programmazione razionale dell’altezza della diga non si basa sul controllo assoluto del futuro (come certo pensiero dominante vorrebbe far credere) ma sulla gestione intelligente dell’incertezza che invece di lavorare contro di noi, ci fornisce una valida mano.
A questo punto il lettore ha in mano gli strumenti concettuali per:
1. Spiegare educatamente a chi (magari in buona fede) pensa che qualsiasi guaio che ci succede sia opera dell’uomo e va in cerca di un colpevole, ricordargli che la natura esiste, è al di fuori di noi anche se ne facciamo parte, è a noi impredicibile al dettaglio dell’evento singolo, ma ci offre delle preziose regolarità.
2. Che la prevenzione si deve basare sulla previsione ‘statistica’ di ciò che ‘potrebbe succedere’ non di cosa succederà di sicuro (compito impossibile), dimensionando le nostre azioni sull’analisi attenta dei dati di natura.






